Category และ Product | Category Theory for Programming Part 1

เมื่อกลางเดือนธันวาคมได้มีโอกาสเอา Category Theory ไปขายใน sharing session ภายในของ LINE แล้วมีคนสนใจมากมาย(ขอบคุณทุกคนมากๆ ที่เข้ามาฟังนึกว่าจะไม่มีไครสนแล้ว T^T) เบื้องหลังการขายครั้งนั้นคือโรงงานนรกที่นั่งปั่นสไลด์พร้อมเพื่อนต้าผู้ช่วยเป็นผู้ซ้อมฟัง เพื่อขัดเกลาสไลด์ให้ดี และพูดได้รักษาเวลาที่สุด

ซึ่งตอนแรก session ขอไป 1 ชั่วโมงแต่ว่าคนลงพูดเยอะมากเวลาเลยถูกแบ่งลงมาเหลือคนละ 45 นาที คราวนี้ด้วยเวลาที่หดสั้นลง เลยต้องตัดสินใจตัดเนื้อหาบางส่วนออก หนึ่งในนั้นคือ product และ co-product เป็นอะไรที่จริงๆ น่าสนใจมากอยากพูดจริงอะไรจริง ไหนๆ แล้วก็เลยมาเขียนเป็นบทความตรงนี้แทน

เพื่อนต้าได้เขียน category theory ในส่วนที่ตัวผมได้พูดไปในวัน sharing แล้ว(เขียนดีซะด้วย) ไปอ่านกันได้ก่อนที่นี่ Category Theory (for Programmer!): บทนำ~จากคณิตศาสตร์สู่ภาษาโปรแกรม

แนะนำอย่างแรงให้อ่านก่อน

---

Category คืออะไรใน Programming ❓

เพราะว่าแคตากอรี่คือแนวคิดที่เป็นนามธรรมมากๆ พื้นฐานของมันมีแค่ object (อ็อปเจ็กต์) และ morphism (มอฟิซึม) จึงสามารถไปประยุกต์ได้หลายสถาณการณ์ หนึ่งในนั้นคือการเอาไปจับกับการเขียนโปรแกรมและกำเนิดเป็นภาษาเชิงฟังก์ชันนอลขึ้นมา

คำถามที่จะเริ่มเกิดขึ้นคือ object ใน category คือส่วนไหนในภาษาโปรแกรมและ morphism เองก็ด้วย ในส่วนนี้เลยจะเริ่มจากอธิบายจุดนี้กันก่อน โดยตัวอย่างทั้งหมดจะใช้ typescript เป็นหลักนะ

🐟 Category of value type

แคตากอรี่ที่เราจะศึกษากันคือแคตากอรี่ที่ใช้โมเดลภาษาโปรแกรมขึ้นมา object ในแคตากอรี่คือ value type (ประเภทของตัวแปร) ในภาษาโปรแกรม ตัวอย่างเช่นในภาษา typescript, อ็อปเจ็กต์ก็จะเป็น number / string / bool (เป็น type ต่างๆ) เป็นต้น

เพราะฉะนั้น value ที่เป็นตัวเลขทั้งหมด ไม่ว่าจะ 0, 1, 2, -1, 0.1, … ล้วนแล้วแต่เป็นอ็อปเจ็กต์ number ทั้งนั้น

อ็อปเจ็กต์ในแคตากอรี ไม่เกี่ยวข้องอะไรกับคำว่าอ็อปเจ็กต์ใน OOP ให้คิดว่าเป็นคนละตัวกันอย่างสิ้นเชิงไม่เกี่ยวข้องกันใดๆ

ความพิเศษของอ็อปเจ็กต์ที่สร้างมาจากชนิดของค่าคือเราสามารถมองเข้าไปในอ็อปเจ็กต์ ได้เพื่อดูว่ามันมีค่าอะไร เช่นค่าตัวเลข 1 เป็นสมาชิกในอ็อปเจ็กต์ number , ค่าตัวเลข 2 แม้ค่าจะไม่เท่ากับ 1 แต่ก็ยังเป็นอ็อปเจ็กต์ number เช่นเดิม

ชื่ออ็อปเจ็กต์ object name	ตัวอย่างค่าที่เป็นสมาชิกของอ็อปเจ็กต์นั้น example value in object
number	0, 1, -1, 0.1, -0.1, ... ค่าเหล่านี้เป็นสมาชิกของ object number ทั้งหมด
string	"hello", "", " ", "world ", ... ค่าเหล่านี้เป็นสมาชิกของ object string ทั้งหมด
boolean	true, false สองค่านี้เป็น object boolean

เมื่อเรามองว่าชนิดของค่าเป็นอ็อปเจ็กต์ในแคตากอรี่แล้ว morphism ก็คือการเปลี่ยนแปลงชนิดของค่า ในภาษาโปรแกรมเรามีเครื่องมือนึงที่ช่วยแปลงชนิดของค่าค่างๆ ได้ นั่นคือ function (ฟังก์ชัน)

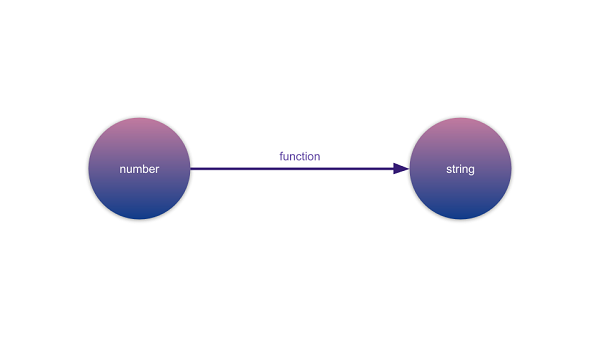ฟังก์ชันทำตัวเป็นมอฟิซึม ที่แปลงอ็อปเจ็กต์นึงไปยังอีกอ็อปเจ็กต์นึงได้

เส้น morphism(มอฟิซึม) ที่ลากจาก number ไปยัง string คือตัวแทนของ function ใดๆ ที่รับอินพุตเป็น number และได้ผลลัพธ์ออกมาเป็น string เช่นสมมติเรามี function ตามตัวอย่างนี้

function foo(x: number): string {
  return x % 2 == 0 ? "even" : "odd"
}

ในมุมแคตากอรี่ของชนิดของค่า นี่คือมอฟิซึมที่แปลงอ็อปเจ็กต์ number ไปเป็น string

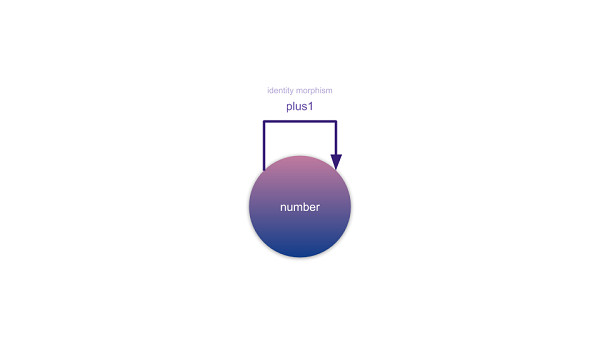
จากกฎของแคตากอรี่ที่ว่าด้วยทุกอ็อปเจ็กต์จะต้องมี identity morphism (มอฟิซึมเอกลักษณ์) ที่เรารู้จักกันในนามของลูกษรที่วกเข้าอ็อปเจ็กต์เดิม ก็จะเป็นฟังก์ชันที่รับอินพุตและคายผลลัพธ์ออกมาด้วยค่าประเภทเดียวกัน

function plus1(x: number): number {
  return x + 1
}

ฟังก์ชัน plus1 รับอินพุตเป็นชนิด number และให้ผลลัพธ์เป็นชนิดเดิมคือ number ดังนั้น plus1 เป็นมอฟิซึมเอกลักษณ์

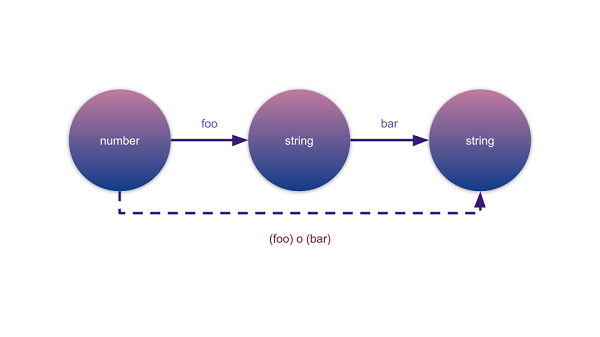
ส่วนกฎข้อที่สองของแคตากอรี่คือการ compose morphism (ประกอบมอฟิซึม) เป็นความสามารถในการสร้างมอฟิซึมใหม่ จากมอฟิซึมเก่าที่มีด้วยการลากเส้นลัด ในภาษาโปรแกรมคือการที่เราสามารถสร้างฟังก์ชันใหม่จากการเรียกฟังก์ชันที่มีหลายๆ ตัวต่อเนื่องกัน

function foo(x: number): string {
  return x % 2 == 0 ? "even" : "odd"
}

function bar(x: string): boolean {
  return x === "odd" ? true : false
}

// compose foo and bar function
function foobar = (x: number): boolean {
  return bar(foo(x))
}

จากตัวอย่างเราจะได้ฟังก์ชันใหม่ที่แปลง number->boolean ด้วยการเอาฟังก์ชันเดิมคือ foo และ bar มาเรียกต่อเนื่องกัน โดยเราตั้งชื่อว่า foobar

☕️ FAQ รวบรวมคำถามที่คนอ่านน่าจะงงเกี่ยวกับเรื่อง Category

รวบรวมคำถามที่มักจะงง และสงสัยเกี่ยวกับ category of type

Question	Answer
ตัวเลข 1 กับ 2 เป็น object เดียวกันหรือไม่	ใช่ครับ ในมุมมองของ category of type เป็นค่าในอ็อปเจ็กต์ number เหมือนกัน
identity morphism คือ function ลักษณะที่รับ input แล้วคืนออกมาเลยไม่ทำอะไรหรือเปล่า (แบบนี้) x => x	function อันนั้นเป็นแค่หนึ่งในตัวอย่างของ identity morphism ครับ ใน category of type เราสนใจแต่ type ครับ ตัว identity morphism คือฟังก์ชันอะไรก็ได้ที่ชนิดของอินพุตและผลลัพธ์ เป็นประเภทเดียวกัน ยกตัวอย่างฟังก์ชันนี้ก็เป็น identity morphism ครับ (x: number) => x + 2 (เป็น identity morphism ของ object number) แสดงว่า identity morphism เนี่ยไม่จำเป็นต้องมีแค่ตัวเดียวครับ ถ้าคุณเคยรู้จักกับ identity การบวกการคูณในคณิตศาสตร์ปกติ ให้มองว่าเป็นคนละเรื่องกันไปก่อนเลยครับจะได้ไม่สับสน
ถ้าอย่างงั้น morphism ระหว่าง object คู่นึง ก็มีได้หลายอันถูกไหม	ถูกครับ ลูกศรที่เชื่อมระหว่างอ็อปเจ็กต์แทนการเปลี่ยนแปลง type นึงไปสู่อีก type นึงซึ่งไม่ได้กำหนดวิธี implement เอาไว้ครับดังนั้นจึงมีได้มากมายหลายหน้าตา
มี category ที่ object ไม่ใช่ type ไหม	มีได้ครับ ขึ้นกับเรานิยามเลย แต่ภาษาเชิง functional จะใช้ category of type เป็น model หลักครับ ถ้าให้ยกตัวอย่าง Set ในคณิตศาสตร์จริงๆ ก็เป็น category นะครับ
แล้วภาษาที่ไม่มี type (dynamic typing) อ็อปเจ็กต์จะหน้าตาเป็นยังไง	ตอนนี้ให้เรามองว่าภาษาแนวๆ นั้นมีอ็อปเจ็กต์เดียวชื่อว่า any ครับ ส่วนฟังก์ชันในภาษานั้นทั้งหมดเป็นมอฟิซึมเอกลักษณ์ไปโดยปริยาย(เพราะมันจะแปลงจาก any -> any เสมอครับ)

มีคำถามเพิ่มเติมแปะไว้ได้เลย เดี๋ยวจะเอามาเพิ่มให้นะครับ

---

Pattern ของ Category 🌼

เพราะว่าแคตากอรี่คือกลุ่มของอ็อปเจ็กต์และมอฟิซึมจับตัวกันเป็นกลุ่ม ถ้าเราลองสักเกตุไปเรื่อยๆ เราจะเห็นรูปแบบบางอย่างขึ้นมาซึ่งเราจะเห็นมันบ่อยๆ และมันมีคุณสมบัติที่น่าสนใจ ถ้าเป็นแบบนั้นเราจะเริ่มตั้งชื่อให้มันเพื่อเอาไปใช้ทำประโยชน์ต่อไป

ตอนนี้เราจะเริ่มจาก pattern แรกที่สำคัญมากๆ ก่อน

✖️ Product (โปรดักต์) ✖️

โปรดักต์เป็นรูปแบบการจับตัวของอ็อปเจ็กต์และมอฟิซึมแบบนึงหน้าตาแบบนี้

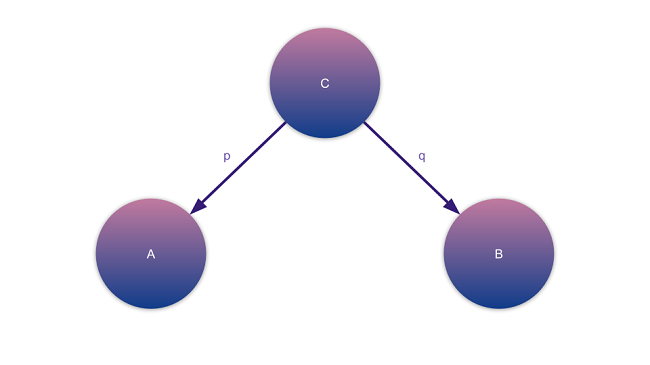
นี่คือรูปแบบแรกที่เราจะมาดูกัน~

เพราะว่าภาษาโปรแกรมถูกสร้างมาจาก category of type เป็นหลัก เหล่าอ็อปเจ็กต์ A, B, C ในแผนภาพก็คือชนิดของค่า จากภาพจะตีความหมายออกมาได้ว่าค่าชนิด C มีฟังก์ชัน p ที่สามารถเปลี่ยนตัวมันให้เป็นชนิด A แถมยังมีอีกฟังก์ชัน q ที่สามารถแปลงมันให้เป็นค่าชนิด B ได้อีก

ในภาษาโปรแกรม C คือชนิดของค่าที่ทำการรวมข้อมูล ชนิดอื่นเอาไว้ในตัวเองสองตัวและมี function ที่ดึงค่าเหล่านั้นออกมาได้

ภาษาโปรแกรมเรามักจะคุ้นกับชนิดของค่าแบบนี้ในชื่อ pair / tuple หรือชนิดของค่าอะไรก็ตามที่สามารถเก็บค่าอื่นๆ ที่ต่างชนิดกัน (หรืออาจจะชนิดเดียวกันก็ได้นะ)สองค่าเอาไว้ในตัวเอง

ถึงเวลาของงานคราฟ เราจะลองมาสร้างอ็อปเจ็กชนิด pair กันจากเริ่มต้นเลย~ (แน่นอน ทำใน typescript นะ)

แต่ก่อนจะไป implement เราจะมีข้อตกลงกันนิดหน่อยเพื่อความเข้าใจง่ายในการ implement

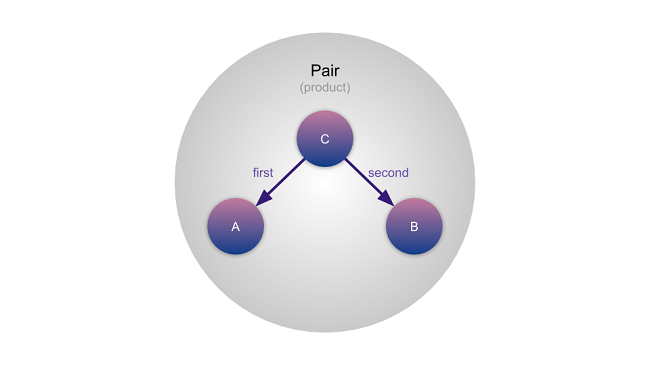
• เราจะให้อ็อปเจ็กต์ C ในแผนภาพมีชื่อว่า Pair (เพื่อความง่ายตอนเอาไป implement เดี๋ยวงง)
• และเราจะให้มอฟิซึม p, q ในแผนภาพเป็นฟังก์ชันชื่อว่า first / second

มาเริ่มจากการสร้าง Pair ก่อนโดยมันคือชนิดของค่าที่บรรจุชนิดของค่าอื่นๆ เอาไว้ในตัวเองสองอัน ใน typescript เราจะใช้ interface ในการสร้างชนิดลักษณะนี้ขึ้นมา

interface Pair { 
    a: number;
    b: string;
}

ตอนนี้เราได้ Pair บรรจุชนิดประเภท number และ string เอาไว้ข้างใน

แต่ถ้าเราสร้างโดย fix type เอาไว้แบบนี้ (ในตัวอย่าง fix เป็น number และ string) แล้วเราจะไม่สามารถสร้าง Pair สำหรับบรรจุชนิดอื่นได้อีกนอกจากเราจะไปสร้างเป็นชื่อใหม่

วิธีแก้ก็คือเราจะปล่อยให้ชนิด ของ a, b ใน Pair เป็น generic type

interface Pair<A, B> { 
    a: A;
    b: B;
}

แบบนี้ Pair เราจะสร้างเพื่อให้บรรจุชนิดอะไรก็ได้แล้ว ชนิดของค่าที่สร้างเข้ามาจะถูกเรียกว่า A และ B แทน (ที่ใช้ A, B เพราะว่าจะได้เหมือนกันภาพโปรดักส์ของแคตากอรี่)

วิธีใช้เราก็กำหนดว่าจะให้เป็น Pair ของ type อะไรด้วยการกำหนดค่าไปได้เลยเพื่อให้ภาษาดึงชนิดออกมาเองอัตโนมัติ (type inference) เสร็จแล้ว A, B จะเป็นตาม type ที่ใส่ค่าเข้าไปเอง

const myPair = {
    a: 10,
    b: "hello"
}

ในที่นี้ A จะเป็นชนิด number และ B จะเป็นชนิด string แบบอัตโนมัติเลยจ่ะ

ต่อไปคือฟังก์ชัน first และ second ใช้ดึงค่าออกมาจาก Pair ตามลำดับ แต่ว่าฟังก์ชันที่สร้างมาจะต้องรับ Pair ซึ่งเป็น generic เพราะเราไม่สนใจว่า Pair จะเก็บค่าข้างในเป็นชนิดอะไรเราแค่ดึงค่าแรก(a) และค่าที่สอง(b)ออกมา

note: ฟังก์ชันที่สามารถรับ input ได้หลายๆ รูปแบบโดยที่การทำงานยังเหมือนเดิมจะมีชื่อเรียกว่า polymorphic function (โพลิมอฟิกฟังก์ชัน)

ใน typescript การที่จะให้ฟังก์ชันรับชนิดของค่าที่เป็น generic ตัวฟังก์ชนั่นเองจะต้องทำเป็น generic ไปด้วย ดูตัวอย่างด้านล่างนี้ได้เลย

function first<A, B>(pair: Pair<A, B>): A {
    return pair.a
}

function second<A, B>(pair: Pair<A, B>): B {
    return pair.b
}

เราก็ใช้ first / second ดึงค่าออกจาก pair ได้

console.log(first(myPair))  // 10
console.log(second(myPair)) // "hello"

เพราะว่า Pair เองก็เป็นชนิดข้อมูลแบบนึงเราจึงมองว่ามันเป็นอ็อปเจ็กต์นึงในแคตากอรี่ได้เช่นกัน

✖️ Nested Product ✖️

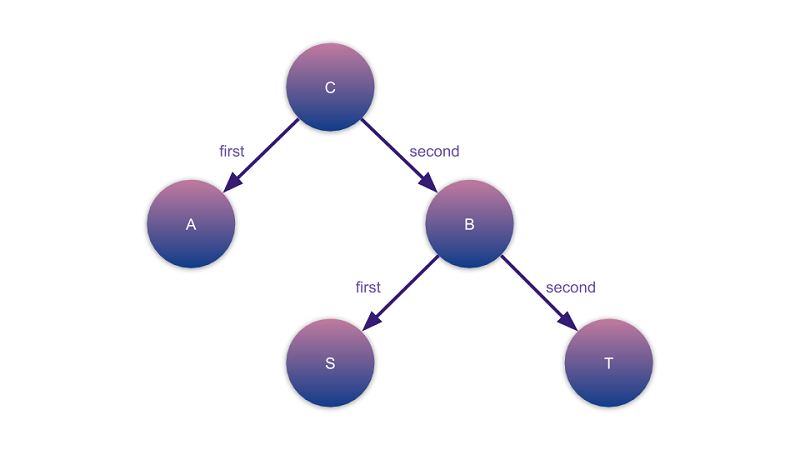
จากรูปแบบ product ข้างต้นเราจะลองสมมติให้ B เป็นอ็อปเจ็กต์ชนิด product แทน เราจะได้หน้าตาตามรูปด้านล่างนี้ เสมือนว่าเราซ้อน product เข้าไปใน product อีกทีนึง

เราลองเช็กดูว่า Pair ที่เรา implement ขึ้นมาก่อนหน้านี้สามารถใช้ในกรณีนี้ได้ไหม

const nestedPair = {
    a: 10,
    b: {
        a: "hello",
        b: false
    } // ตรงนี้เราจะให้ b เก็บค่าที่เป็น pair อีกที
}

console.log(first(nestedPair))            // ได้ 10
console.log(first(second(nestedPair)))    // ได้ "hello"
console.log(second(second(nestedPair)))   // ได้ false

เราจะเริ่มใช้สัญลักษณ์แทนแผนภาพเพื่อความง่ายต่อการเข้าใจ

• เราจะให้ product(pair) เขียนแทนด้วย (A, B) แสดงถึงความหมายว่าโปรดักต์นี้บรรจุข้อมูลชนิด A และ B เอาไว้ตามลำดับ
• ให้ชนิดของค่า B เป็น Pair ไปจะได้ว่าเราสามารถเขียนสัญลักษณ์ได้เป็น (A, (B, C)) (แทนชนิด B ด้วยคู่ (B, C) แทน)

เราซ้อนเข้าไปมากกว่านี้ได้อีกไหม ❓ คำตอบก็คือเราซ้อนกันกี่ชั้นก็ได้เพื่อเก็บข้อมูลเป็นแผงๆ ไม่จำเป็นต้องมีสองตัว (A, (B, (C, D))) (A, (B, (C, (D, ...))))

และนี่ก็คือที่มาของข้อมูลประเภท List / Array ที่เรารู้จักกันเวลาเราเขียนโปรแกรมทั่วไป

จากที่เล่ามาทั้งหมด เราจะได้ไอเดียใหม่ที่ว่าพวกข้อมูลชนิด list ทั้งหลายหรือการรวมข้อมูลเข้าด้วยกันเป็นแพ๊กๆ จริงๆ แล้วมันคือโครงสร้างแบบโปรดักต์ซ้อนๆ กันอยู่นั่นเอง

✖️ Nested Product Isomorphism ✖️

จากแผนภาพ nested product ที่ผ่านมาน่าจะมีคำถามว่าจำเป็นไหมที่ข้อมูล pair ที่ซ้อนอยู่จะต้องไปอยู่ฝั่ง second(ด้านขวาน่ะ) คำตอบก็คือไม่จำเป็นครับ แต่ว่าไม่ว่าเราจะกำหนดให้มันอยู่ด้านไหน ความหมายของการเอาไปใช้ก็จะไม่เปลี่ยนไม่ว่าเราจะซ้อนยังไงก็จะได้ list / array ที่ทำงานได้เท่าๆ กันเสมอ

เราลองดูภาพนี้กันครับ

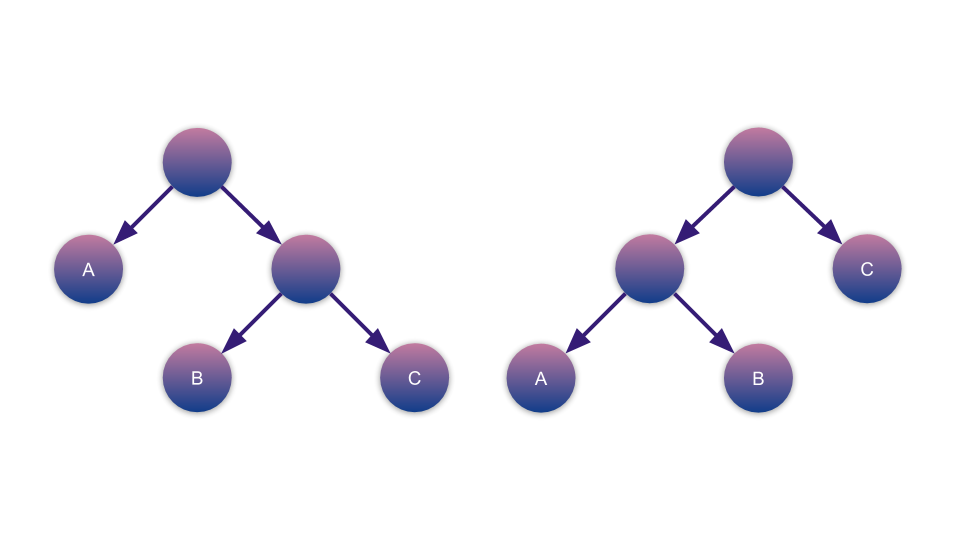
สองภาพนี้เขียนเป็นรูปสัญลักษณ์ได้เป็น (A, (B, C)) และ ((A, B), C) ซึ่งไม่ว่าจะเป็นทางซ้ายหรือขวา ในความหมายของภาษาโปรแกรมคือ

นี่คือชนิดข้อมูลที่บรรจุข้อมูลอื่นๆ เอาไว้ซึ่งลำดับแรกคือข้อมูลชนิด A ต่อมาเป็น B และสุดท้ายคือ C

หรือเราเขียนในรูปสัญลักษณ์ที่เรียบง่ายขึ้นได้เป็น [A, B, C] เพราะจริงๆ ใน list เราสนใจแค่ลำดับของมันเท่านั้น ดังนั้นในแง่ของ list (A, (B, C)) และ ((A, B), C) จะให้คุณสมชัติที่เหมือนกันในทางคณิตศาสตร์เราจะเรียกว่ามัน isomorphic(ไอโซมอฟิก) กัน

เป็นที่มาของภาษาส่วนใหญ่จะไม่ได้ implement ระดับ pair เอาไว้แต่จะสร้างชนิดที่สำเร็จรูปกว่าเอาไว้แล้วคือ list / array แทน แล้วถ้าเราอยากใช้ pair เราก็สร้าง list ขนาดสองแทน

☕️ ช่วง FAQ ของ Product

Question	Answer
ภาษาไหนบ้างที่มี Pair ให้ใช้ตรงๆ	ภาษาส่วนใหญ่จะไม่มี Pair ให้ใช้ตรงๆ เพราะเขาจะไปสร้าง type ที่ใช้แทน pair ได้และมีความสามารถมากกว่าแล้ว
แล้วเราจะรู้เรื่อง Product ไปทำไม	เรารู้เอาไว้ดูไอเดียว่าภาษาโปรแกรมมิงมีที่มาจากแนวคิดแบบไหน สิ่งที่เราใช้กันในปัจจุบันถูกโมเดลมาจากอะไรครับ เปิดโลกดีครับ
Data type แบบไหนในภาษาโปรแกรมปัจจุบันที่เป็นโมเดล product บ้าง	เราจะลองไล่ทีละภาษาเลยนะครับ C/C++: struct Python: tuple Haskell: record typescript: interface javascript: object java: object go: struct อันนี้เป็นตัวอย่างเฉยๆนะครับ จริงๆ product เป็นแค่ไอเดียของการรวมข้อมูล ถ้าเรารวมข้อมูลหลายๆตัวเข้ามาสู่ก้อนเดียวได้ นั่นคือโครงสร้างแบบ product แล้วครับ อย่างเช่น C++ เอง class ก็เป็นโครงสร้างแบบ product เหมือนกันเพราะมันรวบรวมข้อมูลหลายชนิดเอาไว้ในตัวเอง อีกอย่างหลายๆครั้งเราอยากได้ pair เราก็สร้าง array ขนาดสองมาใช้แทนก็ได้ ความหมายเหมือนกัน

Data ที่มีโครงสร้างแบบ product มีความสำคัญมาก เพราะเราสามารถใช้มันประกอบร่างเป็น data structure แบบต่างๆ ได้มากมายเรียกได้ว่าภาษาไหนไม่มีคอนเซ็ปต์ของการแพ็กดาต้าเป็นชิ้นๆ ก็แทบทำอะไรไม่ได้เลย ของมันต้องมีจริงๆ

ของแถม: ในเรื่องเซ็ตของคณิตศาสตร์จะมีสิ่งที่เรียกว่าคาทีเชียนโปรดักต์ อันนั้นเป็นคอนเซ็ป โปรดักต์แบบเดียวกับของแคตากอรี่เลยครับ อย่าลืมว่าเซ็ตก็เป็นแคตากอรี่แบบนึงนะครับ