มาทำความรู้จัก Vector Space กันดีกว่า

ใน Linear algebra หัวข้อ vector space(เวกเตอร์สเปซ) คือส่วนที่เข้าใจยากสำหรับมือใหม่เริ่มศึกษา(เพราะว่ามันเป็น math จ๋ามากๆเลย) แต่เป็นส่วนที่ทฤษฎีที่สำคัญสำหรับการไปศึกษาต่อเรื่องหลังๆ มากดังนั้นบทความนี้เราจะมาพยายามทำความเข้าใจมันอย่างง่ายๆกัน

☄️ อะไรคือ Vector Space

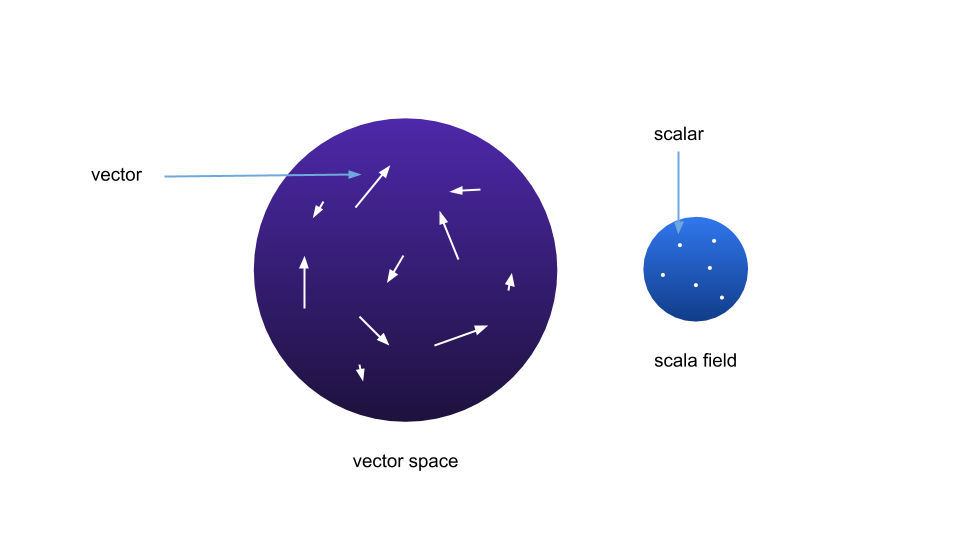
เวกเตอร์สเปซ เราจะแยกออกเป็นสองคำก่อน space(สเปซ) หมายถึงพื้นที่เสมือนใช้เก็บของบางอย่างที่มีคุณสมบัติร่วมกันบางประการ ในที่นี้เราศึกษาเรื่องเวกเตอร์สเปซ ของที่อยู่ข้างในนี้ก็จะถูกเรียกว่าเวกเตอร์

โดยที่เวกเตอร์นั้นให้มองว่าเป็นอะไรก็ได้ แค่มันมีชื่อว่าเวกเตอร์ เพียงเพราะมันอยู่ภายในเวกเตอร์สเปซ ให้เราลืมเวกเตอร์ที่เราเคยเรียนมาไปก่อน

เวกเตอร์สเปซมีพิเศษอีกอย่างนึงคือ นอกจากพื้นที่เก็บเวกเตอร์แล้ว ยังมี “scala field(ฟีลด์สเกล่า)” พ่วงมาด้วยเสมอ แต่เพื่อความง่ายต่อความเข้าใจ เราไม่ต้องไปสนใจว่าฟีลด์คืออะไรในตอนนี้ ให้มองว่ามันเป็นระบบตัวเลขธรรมดาๆ แบบที่เรารู้จักทั่วไปก่อน

📌 คุณสมบัติต่างๆของ Vector Space

เวกเตอร์สเปซมีได้หลายหน้าตา หลายยี่ห้อ แต่ไม่ว่าไครจะสร้างเวกเตอร์สเปซแบบไหนมาจะต้องอยู่ภายใต้ข้อกำหนดเหล่านี้เสียก่อน

การมีอยู่ของการดำเนินการ “บวก” และ “คูณ”

ตัวเวกเตอร์สเปซจะต้องมี operation(การดำเนินการ) อยู่สองแบบ อย่างแรกเราจะเรียกว่า “การบวก” การบวกนี้จะเป็นการบวกกันระหว่างเวกเตอร์ด้วยกันเองสองตัว ส่งผลลัพธ์ออกมาเป็นเวกเตอร์ตัวใหม่ (หรืออาจจะบวกแล้วได้ตัวก็ได้นะ ไม่ได้ห้ามอะไร)

นอกจากนั้นยังต้องมี “การคูณ” แต่การคูณไม่ได้เกิดขึ้นกับระหว่างเวกเตอร์ แต่เป็นการดำเนินการที่เชื่อมระหว่าง เวกเตอร์กับสเกล่า

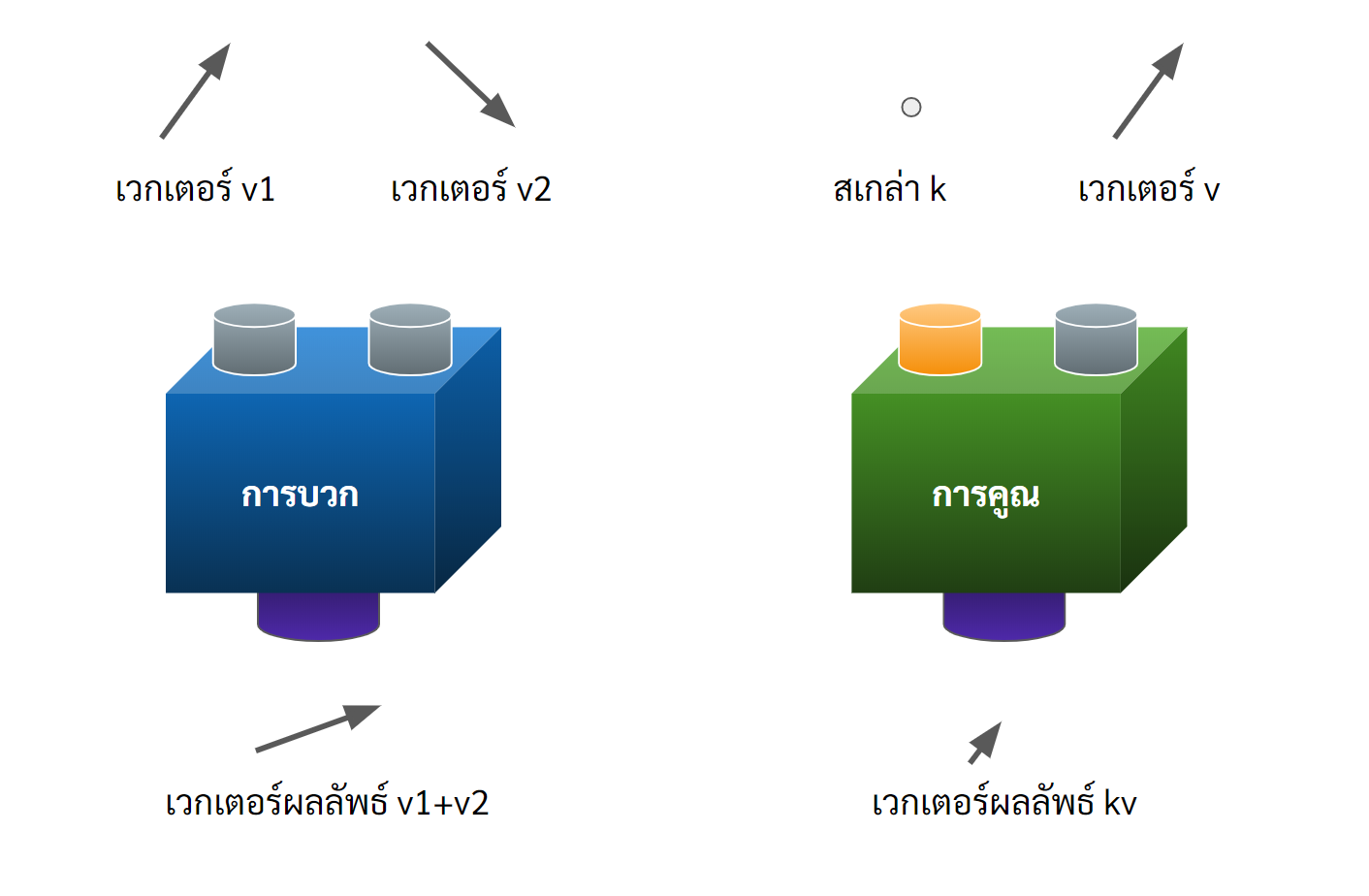
การบวกและการคูณในเวกเตอร์สเปซนี้มีหน้าตาได้หลากหลาย เราอาจจะเจอการบวกแบบพิศดาลได้ในเวกเตอร์สเปซแบบแปลกๆ แต่ไม่ว่ายังไงการดำเนินการพวกนี้ก็ยังมีกฎที่ต้องทำตามอยู่ ไม่ใช่สร้างมามั่วๆยังไงก็ได้

สมบัติปิดของการบวกและคูณ

การจะสร้างการบวกและการคูณมาเราจะต้องมั่นใจว่า ผลลัพธ์จากการบวกและคูณนั้นไม่ว่าเราจะเลือกเวกเตอร์คู่ไหน หรือสเกล่าตัวใดมาบวก/คูณ กันก็จะยังอยู่ในเวกเตอร์เสปซเดิมอยู่ ไม่ได้กระเด็นออกไปที่ไหน

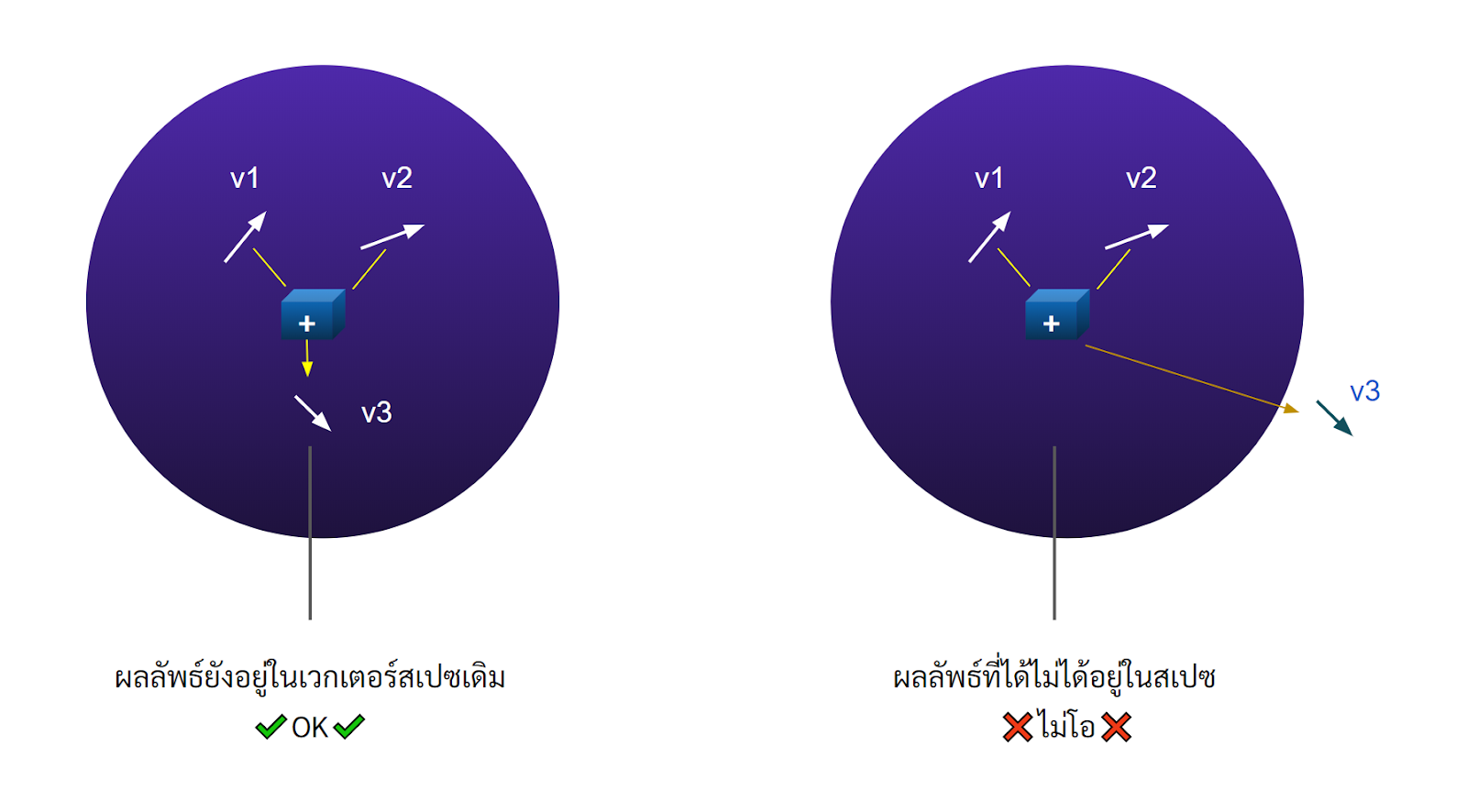
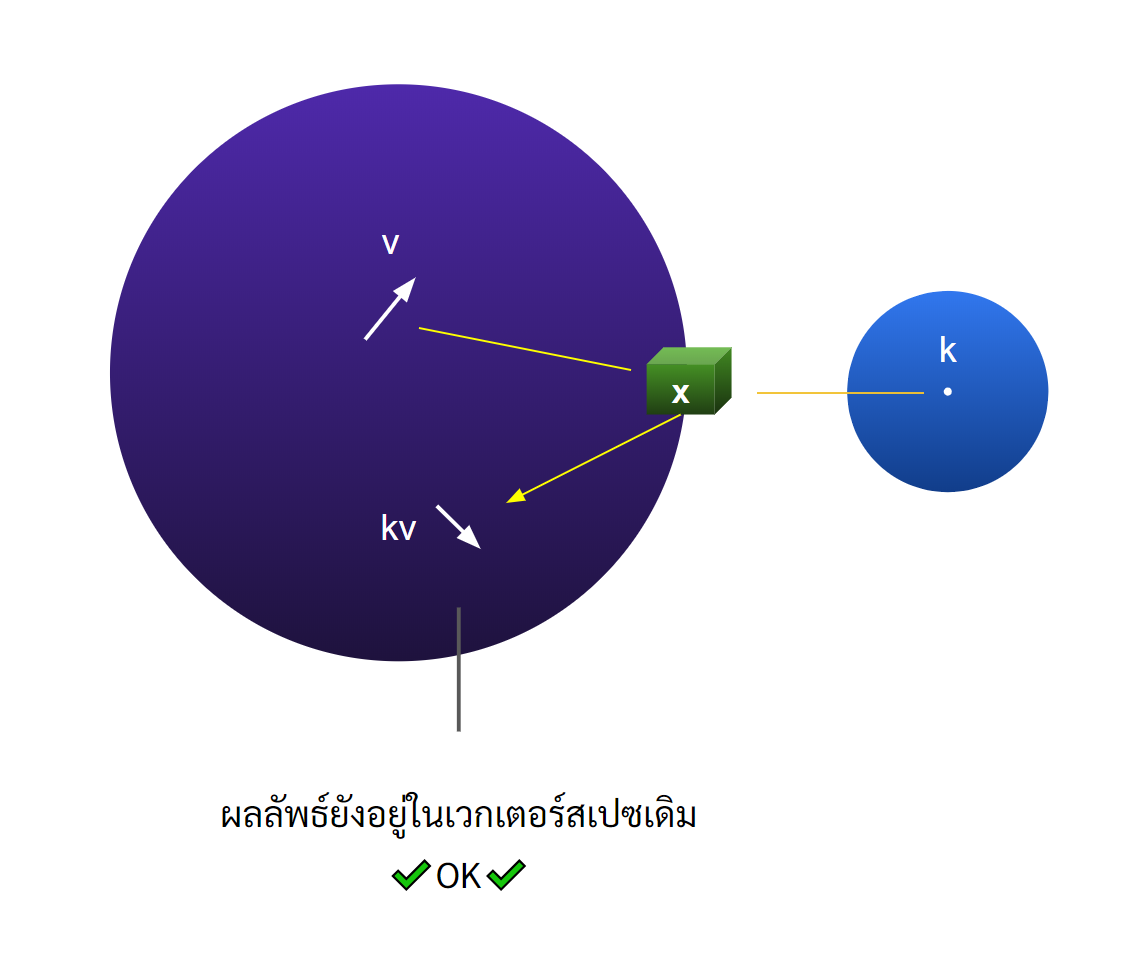
เราเรียกคุณสมบัติแบบนี้ว่า สมบัติปิด (closed)

สมบัติของการสลับที่และการเปลี่ยนหมู่

ถ้าเราเคยชินกับการบวกและคูณในระบบจำนวนจริง เราจะนึกได้เลยว่าเราสามารถสลับที่การบวกได้ก็คือไม่ว่าเราจะเอาตัวเลขไหนขึ้นก่อนในการบวก ผลลัพธ์ก็ได้เท่าเดิม

ในหัวข้อนี้จะให้ u v w แทนเวกเตอร์ และ k l แทนค่าสเกล่า

$$ v + u = u + v $$

นอกจากนั้นถ้าการบวกเกิดขึ้นมากกว่า 1 ในทั้งเดียวเราสามารถคำนวณค่าของคู่ไหนก่อนก็ได้ ก็คือ

$$ v + u + w = (u + v) + w = v + (u + w) $$

ทั้งสองคุณสมบัตินี้ก็ต้องมีในการบวกเวกเตอร์เช่นกัน

สำหรับการคูณนั้นจะแตกต่างจากระบบจำนวนจริงนิดนึง เพราะมันเป็นการเอาสเกล่าเข้ามาคูณกับเวกเตอร์ ดังนั้นสมบัติที่จะต้องมีจะเป็นลักษณะนี้แทน

$$ klv = (kl)v = k(lv) $$

เราจะเรียกว่า การบวกและคูณมีสมบัติการสลับที่(cumulative) และเปลี่ยนหมู่(associativity)

ผมจะยกตัวอย่างการสร้างเวกเตอร์สเปซของผมขึ้นมา ผมจะสร้างเวกเตอร์เสปซที่เก็บ “คู่อันดับ” โดยมีการบวกแบบแปลกๆ ที่ผมคิดขึ้นมาเองแบบนี้

$$ (a, b) + (c, d) = (2a + c, b + d) $$

การบวกที่ผมตั้งใจสร้างขึ้นมานี้ไม่สามารถใช้ได้ เพราะขัดกับกฎ การสลับที่

ตัวอย่างคือถ้าเราลองดูเวกเตอร์สองตัวในสเปซ (2, 1) และ (3, 0) ถ้าผมจับบวกกันในแบบของผมเองจะได้ผลลัพธ์เป็น (7, 1)

ขณะที่เมื่อผมสลับที่แล้ว (3, 0) + (2, 1) จะได้ผลลัพธ์เป็น (8, 1) ซึ่งมันไม่เท่ากัน

สมบัติการกระจาย/แจกแจง

เมื่อเราเอาสเกล่ามาคูณกับเวกเตอร์ที่บวกกันอยู่ จะมีค่าเท่ากับการที่เอาสเกล่าเข้าไปคูณเวกเตอร์ทีละตัว ดังนี้

$$ k(u + v) = ku + kv $$

เหมือนในระบบเลขที่เราชินกันเลย แต่ u กับ v เป็นเวกเตอร์เท่านั้น และ k ก็จะต้องเป็นสเกล่า (เพราะการคูณทำได้เฉพาะสเกล่า-เวกเตอร์)

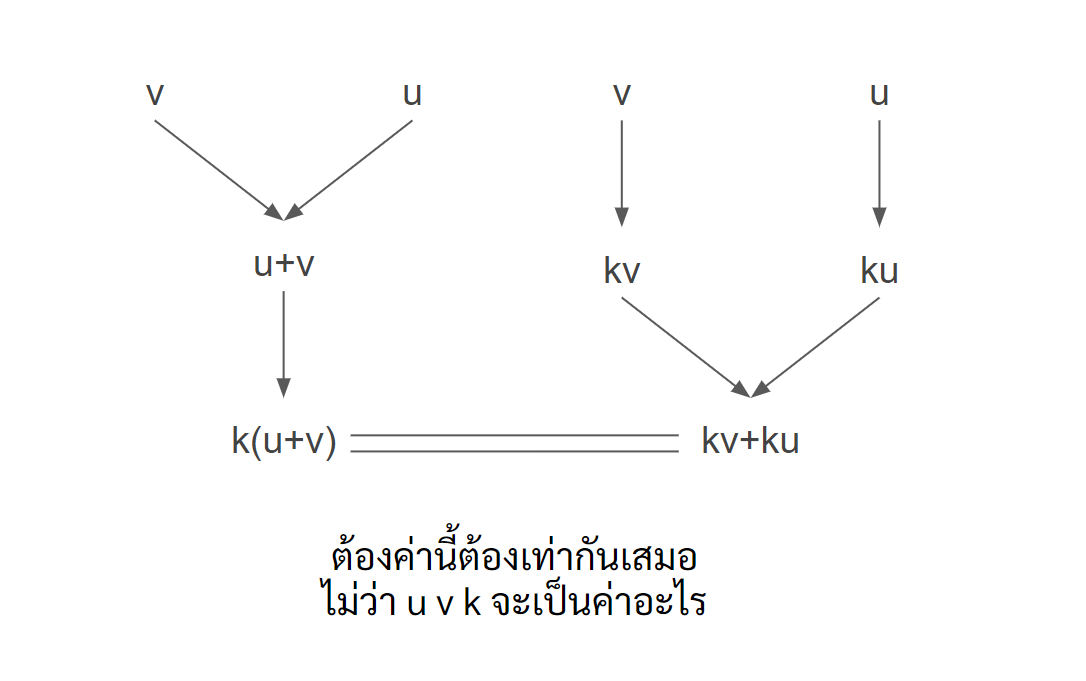
เรามีชื่อเรียกคุณสมบัติแบบนี้ว่า สมบัติการแจกแจง(distributive)

การมีอยู่ของสมาชิกเอกลักษณ์

สมาชิกเอกลักษณ์(identity) คือเวกเตอร์ที่มีพฤติกรรมพิเศษก็คือ “เอาไปบวกกับเวกเตอร์อะไรในสเปซ ก็ได้ผลลัพธ์เป็นเวกเตอร์เดิม” ถ้าในระบบจำนวนจริงก็อารมเลข 0 นั่นแหละ ในเวกเตอร์สเปซของเราจะต้องมีเวกเตอร์ที่มีสมบัตินี้อยู่ และจะต้องมีเพียงตัวเดียวด้วย

สมมติว่าผมสร้างเวกเตอร์สเปซขึ้นมาเอง เป็นคู่อันดับเหมือนเดิม (a, b) การบวกของผมกำหนดให้เป็นการบวกแปลกๆ แบบนี้

$$ (a, b) + (c, d) = (a + c, b + d + 1) $$

สมาชิกเอกลักษณ์ของผมก็จะได้เป็น $ (0, -1) $ เพราะสำหรับทุก a, b ไม่ว่าจะเป็นค่าอะไร

$$ (a, b) + (0, -1) = (a + 0, b + -1 + 1) = (a, b) $$ และ $$ (0, -1) + (a, b) = (0 + a, -1 + b + 1) = (a, b) $$

เสมอ

ถ้ามีคนบอกว่านี่คือเวกเตอร์สเปซ เราจะหาสมาชิกเอกลักษณ์ในนั้นได้เสมอ และถ้าเราจะสร้างเวกเตอร์สเปซเราก็ต้องทำให้มันมีสมาชิกเอกลักษณ์ด้วย

การมีอยู่ของคู่สมาชิกผกผัน

อันนี้จะต่างจากเอกลัฏษณ์หน่อยตรงที่ เอกลักษณ์คือสมาชิกหนึ่งตัวในเสปซที่มีคุณสมบัติตามที่ว่ามาข้างต้น แต่ว่าสมาชิกผกผันจะไม่ได้เป็นแบบนั้น

สมาชิกผกผัน(inverse) จะอยู่ในรูปของคู่สมาชิกกับเวกเตอร์ที่เราสนใจ เช่นในเสปซเรามีเวกเตอร์ชื่อ $v$ เราจะต้องหาสมาชิกผกผันของมันได้ และเรียกมันว่า $v^{-1}$ (อ่านว่า อินเวอร์สของ v หรือ ผกผันของ v)

สมาชิกผกผันไม่ใช่เราจะหามาแบบส่งๆยังไงก็ได้ แต่มีกฎอยู่ว่ามันจะเป็นสมาชิกผกผันก็ต่อมือเอาไปบวกกันแล้วได้เอกลักษณ์เช่น สมาชิกผกผันของ $v$ คือ $v^{-1}$ แล้วเราจะได้ว่า เมื่อมันบวกกันจะได้เป็นเอกลักษณ์เสมอ

$$ v + v^{-1} = e = v^{-1} + v $$

นอกจากนั้นทุกเวกเตอร์ในสเปซเราจะต้องหาคู่ผกผันของมันได้

🖍 ตัวอย่างของเวกเตอร์สเปซ

เราพูดถึงลักษณะของเวกเตอร์สเปซกันมาหมดแล้ว เราจะมาดูตัวอย่างเวกเตอร์สเปซกันบ้าง

เวกเตอร์	การบวก	การคูณสเกล่า	เอกลักษณ์	ผกผันของ v
คู่อันดับ $(a,b)$	การบวกคู่อันดับ $(a,b) + (c,d) = (a+c, b+d)$	$k(a,b) = (ka, kb)$	(0,0)	$(a,b)^{-1} = (-a,-b)$
เมทริกซ์ $\begin{bmatrix}a_{11} & a_{12}\a_{21} & a_{22}\end{bmatrix}$	$\begin{bmatrix}a_{11} & a_{12}\a_{21} & a_{22}\end{bmatrix} + \begin{bmatrix}b_{11} & b_{12}\b_{21} & b_{22}\end{bmatrix} = \begin{bmatrix}a_{11} + b_{11} & a_{12}+b_{12}\a_{21}+b_{21} & a_{22}+b_{22}\end{bmatrix}$	$k(a,b) = (ka, kb)$	(0,0)	$(a,b)^{-1} = (-a,-b)$
พหุนาม $a_0 + a_1 x + a_2 x^2$	การบวกพหุนาม $a_0 + a_1 x + a_2 x^2 + b_0 + b_1 x + b_2 x^2$	$k(a_0 + a_1 x + a_2 x^2) = k a_0 + k a_1 x + k a_2 x^2$	0	$-1(a_0 + a_1 x + a_2 x^2) = -a_0 - a_1 x - a_2 x^2$

🎁 Wrap up 🎁

หากคุณอยากมีเวกเตอร์สเปซเป็นของตัวเอง เริ่มกำหนดดังขั้นตอนนี้

• คุณต้องมีเซตเก็บเวกเตอร์ ลองกำหนดเวกเตอร์ขึ้นมาดูนะ
• คุณต้องมีเซ็ตเก็บสเกล่า เพื่อความง่ายให้มองเป็นตัวเลขธรรมดาไปก่อน สร้างมาเพื่อเอาไว้คูณกับเวกเตอร์เฉยๆ
• สร้างการบวกระหว่างเวกเตอร์ขึ้นมา ให้แน่ใจว่าเมื่อบวกแล้วยังเป็นเวกเตอร์ในเซตที่กำหนดอยู่
• สร้างการคูณระหว่างเวกเตอร์กับสเกล่ามา เช่นเดียวกันกับการบวก คูณแล้วยังต้องเป็นเวกเตอร์นะ
• การบวกต้องสลับที่ได้ เปลี่ยนหมู่ได้ นอกจากนั้นยังกระจายกับการคูณได้คล้ายๆกับเลขปกติที่เรารู้จักทั่วไป
• อย่าลืมสมาชิกเอกลักษณ์ และ คู่สมาชิกผกผัน

ลองสร้างเวกเตอร์สเปซดูนะ

การที่เรารู้ว่าสิ่งนี้เป้นเวกเตอร์สเปซ จะทำให้เรารู้คุณสมชัติต่างๆของมันเพิ่มอีกมากมาย เช่น ความเป็นอิสระ มิติ ค่าไอเกน การแปลง

ดังนั้นมันเลยเป็นโครงสร้างที่สำคัญมากๆ เรียกได้ว่า linear algebra นี่ศึกษาเวกเตอร์สเปซกันเกือบทั้งเรื่องเลยทีเดียว